引子
最近痴迷于用Python进行各种随机实验(概率与统计真的太好玩了),甚至尝试用一些蒙特卡洛和数值模拟的方法验证一些数学Theorem。本文将记录我对随机游走定理的实验验证。
先简单介绍一下这个定理。随机游走定理指出,在一维或二维空间中,从起始点出发进行随机运动的点会无限次回到起始点,也就是具有“常返性”;而在大于等于三维的空间中,随机运动的点不具有“常返性”。不具有常返性,不是指不会回来,而是每回来一次,再次回来的概率就会越来越小,直至趋于0。直观上看,就是这个点在回到起始点若干次(也有可能一次都没有)之后,它再也不会回来,而是往原理起始点的方向“扩散”开去。
匈牙利数学家P´olya在1921年证明了该定理,所以这个定理有时候被称为P´olya’s Random Walk Theorem或Po´lya’s Recurrence Theorem。日本著名数学家角谷静夫通俗形象地将Po´lya随机游走定理表述为:喝醉的酒鬼总能找到回家的路,但是喝醉的鸟不能。虽然这个描述有失准确,但是深入人心,因此也有人称该定理为“酒鬼回家定理”。
我在阅读了随机游走定理的一个证明1之后,萌生了通过Python进行模拟实验验证的想法。本文记录了验证的方法和实验结果。
模型建立
随机游走问题的深入分析
我们首先需要建立一个可以准确表述和分析随机游走定理的数学模型。在一个N维空间中有一个点,称其为“粒子”(仅仅只是数学上的点),不妨设这个点的起始坐标为
随机游走定理的一个前提是,粒子具有无限长的运动时间,也就是粒子可以移动无限步。随机游走定理指出,在一维和二维晶格中,粒子出发后会以100%的概率回到原点,然后再次离开,那么根据随机游走定理,它一定会第二次回来……它会无限次回到原点。而在大于等于三维的空间中,随机游走的点回到原点的概率小于1。假设粒子出发后第一次回到原点的概率是
假设我们能进行N维晶格上随机游走的实验,能够观察无限长的时间并记录粒子的回归次数。而且我们可以进行无限次独立的实验观测。对这无限次观测的结果求平均(其实就得到了期望),我们会发现在一维和二维空间中,回归次数是无限大,而在大于等于三维的空间中回归次数的平均值是一个有限的正实数。当然我们不可能实现这样的理想实验,因为这里有两个“无限”,但是我们可以用较长的时间和较大量的实验次数去近似理想实验。并且从实验结果中观察到“趋于无穷”或“收敛于有限”的趋势。
有限的模型
在计算机中,很容易实现一个有限步随机游走的模拟实验。把N维晶格中的粒子抽象成一个整数数组,这个数组代表了粒子的坐标。每次移动就是对数组中的随机一个数加1或减1。在每次实验中让坐标从原点开始“移动”
一个较困难的问题是,要对这样的模拟实验进行怎样的统计,并从统计结果中观察出随机游走定理的结论。如果直接统计回归次数并取平均,那么存在一个问题,随着实验次数的增加,我们得到的平均值其实是在接近
于是我设计了这样一个统计量,对一次有限随机游走实验,统计一个数值序列
在
实验
首先给出实验的代码
1 | import numpy as np |
上述代码省略了画图的部分,并只展示了一维情况下的实验。对一二三维情况下的统计情况的可视化如下(因为只要证明了三维是收敛的,四维就是同理可得了,所以我没有做更高维度的实验)
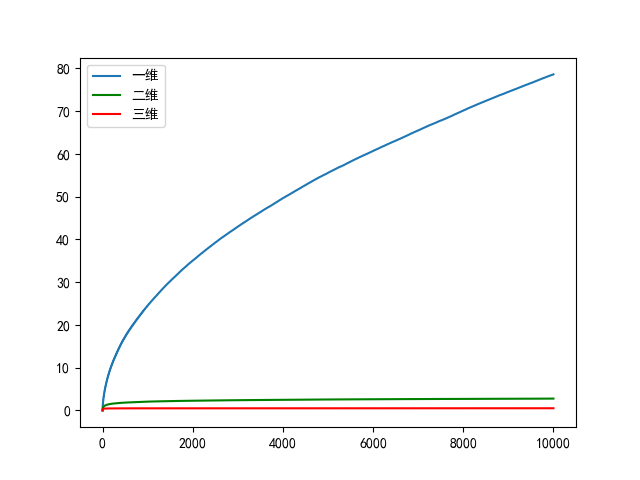
可以看到一维情况下,曲线明显是发散的。但是肉眼难以判断二维和三维的曲线变化趋势。我把二维和三维的曲线图单独拉出来对比如下
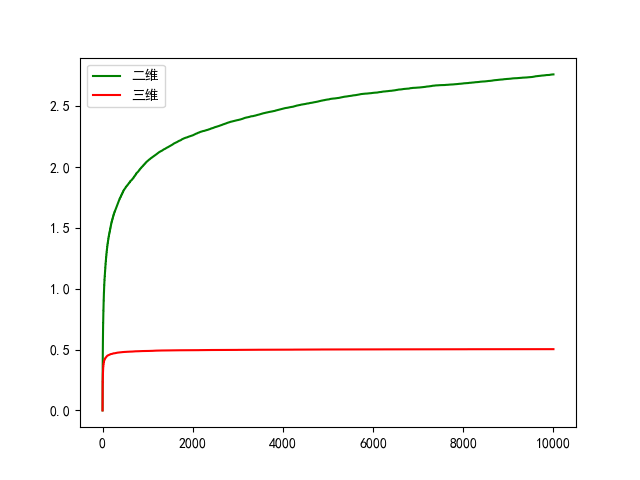
二维的曲线增长接近对数曲线,即二维的
上述实验分析验证了我们的猜想。
总结
本文通过模拟实验验证了P´olya随机游走定理,和理论证明相比,实验验证的优势是直观易懂,无需高等的数学知识和技巧,而且能估计得到大于等于三维情况下的回归次数期望的数值结果。
参考
- [1] 喝醉的酒鬼能找到回家的路吗?
- [2] 理论证明
- Post title:N维随机游走的常返性模拟实验验证
- Post author:shaw
- Create time:2021-08-09 17:15:53
- Post link:https://www.zenwill.top/2021/08/09/N维随机游走的常返性的模拟实验验证/
- Copyright Notice:All articles in this blog are licensed under BY-NC-SA unless stating additionally.