引子

黎曼函数⁷定义为一个无穷级数

函数在黎曼的素数分布的理论¹及大名鼎鼎是黎曼猜想²中占据了重要的地位。但是原始的定义在，而解析数论中所使用的函数定义在几乎整个复平面上（除了极点），因此严格意义上讲他们不是一个函数，因为定义域不同。但是在定义域重叠的部分，函数取值是一致的，所以后者实际上是前者的解析延拓。解析延拓是复变函数理论中用于扩展函数的定义域的方法，为函数在未定义的区域上赋值，并且使拓展后的函数依然满足满足全纯或亚纯等条件。黎曼是最先对函数进行解析延拓的数学家，并发现延拓后的函数的零点的分布情况（黎曼猜想指出函数的所有非平凡零点满足）与素数的分布情况存在密切的联系⁵。且不论黎曼猜想对后世数学发展的影响，任何完整但粗浅地了解过黎曼的这一工作的人都会为黎曼光辉耀目的直觉所折服。

黎曼素数计数函数随着非平凡零点项的增加而变精确

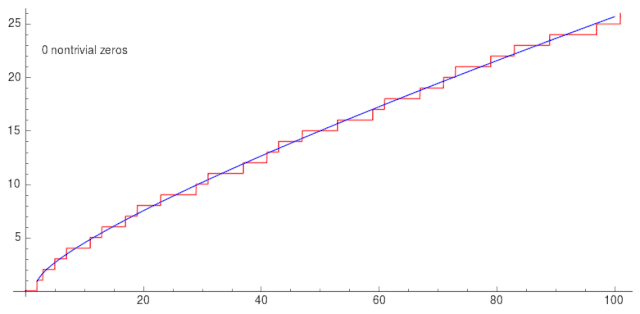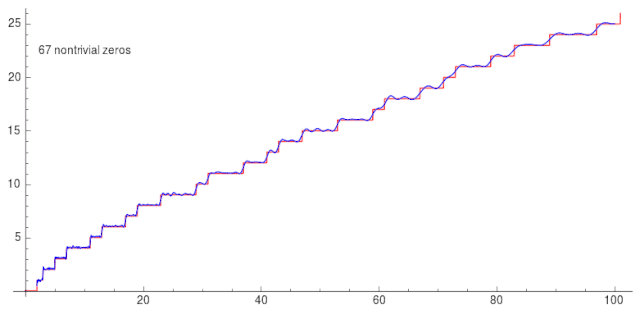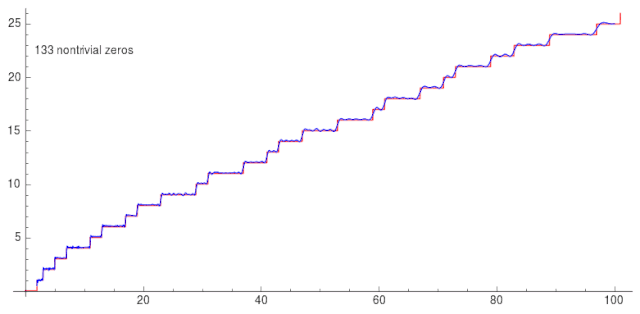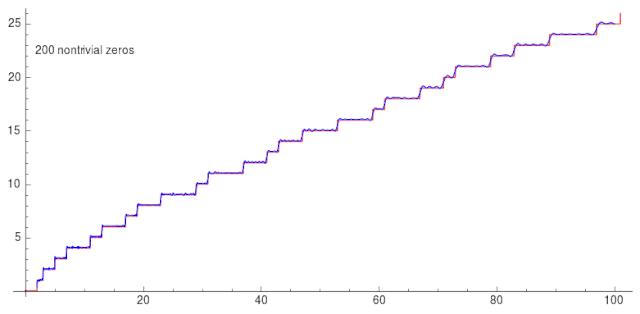
除了黎曼在其论文中提出的延拓方法，还存在一些其他的延拓方法。本文将对我在一些资料中所接触到的延拓方法进行总结整理。

准备工作

在开始介绍函数的解析延拓方法之前，先做一些概念和工具上的铺垫。

首先注意到，是调和级数，他是发散的。欧拉证明了对于实数，是收敛的。可以证明，对复数，若其实部大于1，即满足，函数也是收敛的。所以函数的定义域可以自然扩展到复平面上的区域。

定义多重对数函数（Polylogarithm）⁶

以及伽马函数(阶乘函数的解析延拓函数，由欧拉提出)

根据性质（推导见³

可以得到

由此我们得到了函数的积分形式，注意到这一积分形式并没有拓展函数的定义域，仍然是。

类似的，我们可以得到另外一个关系式

这里出现了一个新的函数（Dirichlet eta function⁸，它也是一个无穷级数和。函数和函数关系密切，可以观察到，无论是级数形式还是积分形式，这两个函数都存在很明显的对称性。在级数形式中，使函数的每一项正负号交替即可得到函数，因此函数也被称为alternating zeta function。欧拉也研究过函数，并且证明了它的定义域为，也就是在这个区域上级数收敛，另外注意到，积分形式的定义域为。

可以证明函数和函数存在关系

因为相当于函数中的所有偶数项，因此从函数中减掉两倍的偶数项，即得到正负交替的级数和。

整理上式得

上面的关系虽然是从级数形式中证明得到的，但是对于积分形式也是成立的（废话！）。注意到这一关系式实际上将函数的定义域延拓到了。

函数的解析延拓

黎曼的方法

黎曼在其论文中通过路径积分对函数进行了解析延拓¹

其中积分路径由三部分组成：
1.从正无穷沿着正实轴到一个很小的正数
2.以原点为圆心，逆时针旋转一圈
3.从沿着正实轴到无穷远处
最后取极限

积分路径

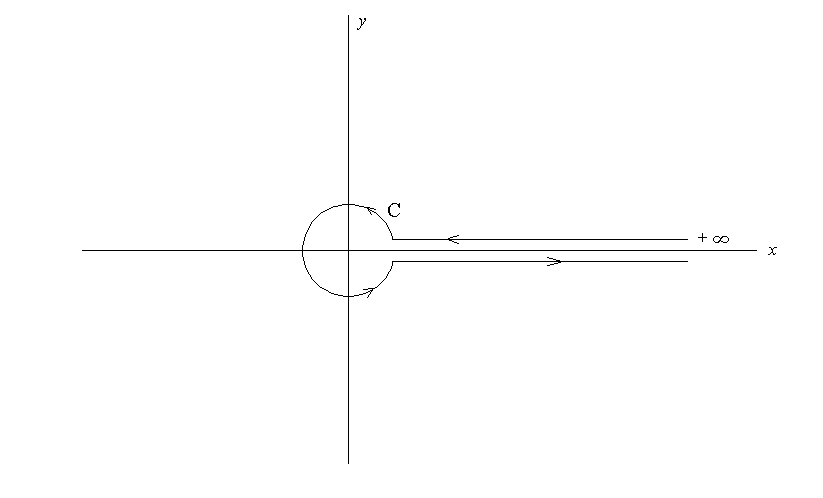
通过对称性进行延拓

我们已经通过函数和函数的关系将函数的定义域扩展到了，进一步研究函数，可以发现其在的区间内存在某种对称性（对称轴为）。这种对称性具体表现为Riemann’s functional equation

或者等价形式

注意到上式可以帮助我们把函数的定义域拓展到的区域，因为等号右边的是有定义的。

Riemman本人给出了Riemann’s functional equation的两种证明方法，后人也给出了各种证明方式。这里简单介绍两种：
1）通过拉式变换和柏松求和，得到对称性（具体见⁴）
2）Hardy证明了用函数表达的Riemann’s functional equation在的区间成立^{9. pp. 16-17}

最后利用对称性写分段函数完成延拓

易知，该分段函数的定义域为。利用上式，我在Python中实现了函数，并与第三方包中实现的函数进行了比较，误差在允许范围内，验证了实现的正确性。代码如下

import numpy as np
from scipy.integrate import quad
import mpmath as mp
mp.dps = 100
mp.pretty = True

def quadc(func, a, b, args):
    """
        help function to attain integration 
        of a complex-valued function
    """
    def real_func(x):
        return np.real(func(x, *args))
    def imag_func(x):
        return np.imag(func(x, *args))
    real_integral = quad(real_func, a, b)
    imag_integral = quad(imag_func, a, b)
    return real_integral[0] + 1j*imag_integral[0]

Gamma = lambda s: \
quadc(lambda x, s_: x**(s_-1) * np.exp(-x), 0, np.inf, args=(s, ))

I1 = lambda s: \
quadc(lambda x, s_: x**(s_-1) * np.exp(-x)/(1 - np.exp(-x)), 0, np.inf, args=(s, ))

I2 = lambda s: \
quadc(lambda x, s_: x**(s_-1) * np.exp(-x)/(1 + np.exp(-x)), 0, np.inf, args=(s, ))

def zeta(s):
    """piecewise function"""
    if np.real(s) > 1:
        return I1(s) / Gamma(s)
    elif np.real(s) >= 0:
        return I2(s) / (Gamma(s) * (1 - 2**(1-s)))
    else:
        return 2**s * np.pi**(s-1) * np.sin(np.pi*s/2) * Gamma(1 - s) * zeta(1 - s)

s = -1 / 2 + 1j
print(zeta(s))
# Output: -0.0008178931310828252 - 0.22307168869792196j
print(mp.zeta(s))
# Output: -0.000817893132952545 - 0.223071688697778j

利用阿贝尔求和法

我在阅读相关资料的时候，猜测得到了另外一种延拓方法，并使用Python进行了验证。在我接触到资料中，未有明确地提出此种延拓方法，但是据我所知，欧拉在研究函数和函数时用到了这一方法。利用这一方法，欧拉得到了一个“著名悖论”———自然数求和公式，这个等号实际上不成立，严谨的表述应该是，其中函数的定义域为。

自然数求和公式的左侧是一个发散的级数和，事实上，对于对于复数，当时，都是一个发散的级数和。数学中存在专门为发散级数确定（赋值）有限的和的方法¹⁰。这种方法实际上是不严谨的，甚至是有害的，正常情况下应该通过解析延拓等方法绕过处理发散级数的问题（物理学家们经常使用发散级数求和的技巧，如重整化方法等）。N. H. Abel曾说

Divergent series are in general something fatal, and it is a disgrace to base any proof on them.

可见除非迫不得已，或者是为了在不严谨的语境下洞见某种规律（正如欧拉所做的），数学家一般不接受通过发散级数求和方法来研究问题。因此我尝试研究此类方法，完全是出于个人兴趣。

阿贝尔求和法¹⁰可以用来处理是一个发散级数的情况。对于发散的无穷级数，阿贝尔和定义为

我们可以通过阿贝尔求和法为函数在定义域上确定函数值。我用Python验证了这样的想法

s = -1 / 2 + 1j
eta = 0
for i in range(1, int(1e10)):
    eta += i**(-s) * (-1)**(i + 1) * (1 - 1e-4)**i
    zeta2 = eta / (1 - 2**(1-s))
    print(np.real(zeta2) * 12)
# Output: -0.0008262168997433036-0.2230608774298546j

对比上一小节的结果，误差在可接受范围内；通过上面的代码，我还验证了自然数求和公式的结果。通过计算机程序，验证了这样的延拓方法在数值计算上是有效的。

另外，欧拉通过阿贝尔求和法，也发现了Riemann’s functional equation的等价形式。
欧拉发现的Riemann's functional equation的等价形式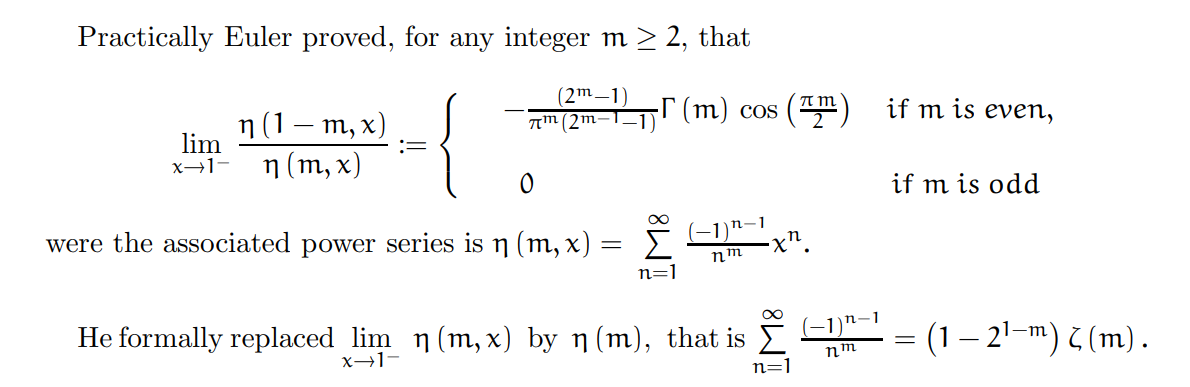

小节

函数真美啊。
$Riemann's $\zeta$ function的可视化图像$

参考

[1] Riemann, Bernhard (1859). “Über die Anzahl der Primzahlen unter einer gegebenen Grösse”
[2] Wiki on “Riemann Hypothesis”
[3] 读懂黎曼猜想（2）——Mellin变换、素数计数函数、与欧拉乘积
[4] 读懂黎曼猜想（3）——平凡零点、非平凡零点与黎曼猜想
[5] 读懂黎曼猜想（5）——精确公式和素数计数函数的渐近展开
[6] Wiki on “Polylogarithm”
[7] Wiki on “Riemann zeta function”
[8] Wiki on “Dirichlet eta function”
[9] E.C. Titchmarsh, The Theory of the Riemann Zeta Function, Oxford Univ. Press, 1951
[10] Wiki on “Divergent series”